Problem Spotlight: Random Numbers
Introduction
But surprisingly, random numbers aren't just useful for entertainment. Randomized algorithms can be much more powerful than fully deterministic ones. This is commonly seen in search and optimization algorithms. Greedy algorithms and gradient descent are powerful tools, but randomness lets us improve them by reducing tendency to get stuck in locally optimal points or searching spaces where it is hard to define gradients.
Even many problems that seem highly deterministic can be solved better using randomness. Number theory has a lot of examples of this: fast factorization algorithms like Pollard's Rho algorithm, Lenstra's Elliptic Curve algorithm, and special/general number field sieves; square root algorithms like Cipolla and Shanks; some prime testing algorithms like Miller Rabin; and so on.
The theoretical power of randomized and fully deterministic algorithms is a more fine grained version of the famous $P$ vs $NP$ problem (though the practical power of randomized algorithms is undisputably higher, with the notable caveat that pseudorandomness is usually sufficient). $P$, $ZPP$, $RP$, $BPP$, $BQP$, and $NP$ are all complexity classes, representing problems which can be solved in polynomial time by different kinds of computers.
- $P$ is the set of yes/no problems that can be solved in polynomial time on a fully deterministic computer. The AKS prime testing algorithm is polynomial time on such a computer, proving prime testing is in $P$.
- $ZPP$ - a computer with access to random numbers.
- $RP$ - a computer with random numbers that may have false negatives less than half the time (but never false positives). The Miller Rabin prime testing algorithm is polynomial time in such a setting, proving prime testing is in $RP$ (but we know the stronger result that it is in $P$).
- $BPP$ - a computer with random numbers that may have false positives and false negatives with less than a third of the time.
- $BQP$ - a quantum computer. Shor's algorithm is polynomial time in this setting, so factorization is definitely in $BQP$, though it may be in one of the above classes too.
- $NP$ - a nondeterministic computer. Nondeterminism computers can't actually exist and are only a theoretical tool.
However, in practice there are a lot of problems that we know how to solve quickly with randomness but not without it, so unless it turns out $P=NP$ in a way we can actually take advantage of, randomized algorithms will remain useful.
Looks Random to me
While there are several ways to obtain truly random numbers on computers, they all have some drawbacks and tend to be slow, so pseudorandom numbers are used instead whenever possible. Reasonably non-vintage x86 processors have hardware random number generators based on electrical noise, external hwrngs exist, Linux and other operator systems implement true random number generators using "entropy pools" constructed from user input, network activity, and other unpredicatable sources, and online services using their own hwrngs exist. All of these require trust, and vulnerabilities have been found in Linux's rng in the past.
But what does it really mean for numbers to be random? How can we create prngs that operate deterministically but emulate true randomness? The answer is that nobody really knows. In mathematics, probability and statistics are built on the foundation of equally likely outcomes and probability spaces. Different elements of some set are assigned different probabilities, and how we actually generate these elements is not really the concern of probability and statistics. However, we can use the math to come up with tests of how random things are.
For instance, if we generate a huge number $n$ of random bytes, we expect each possible value of a byte to occur $\frac{n}{256}$ times. We can then use some prng we wish to test to make many such bytes, and use a goodness of fit test like Chi-Squared to tell us what the probability of getting the bytes we saw from a true randoum source would be. We can also check the correlation between bytes at different offsets to ensure they are very low. Checking for uniformity and non-correlation in many transformations of the output of a prng is pretty effective, and a lot of prng tests boil down to this.
Order, through a Kaleidescope
This ability to recover the "seed" (internal state) from a recurrence based prng is quite interesting. Let's explore this kind of prng more so we can understand this.
In a very general sense, we can think of recurrence based prngs as taking some smooth and easy to understand curve like a straight line or an elliptic curve, and projecting it down from the real numbers to some finite field where its structure becomes completely undetectable.
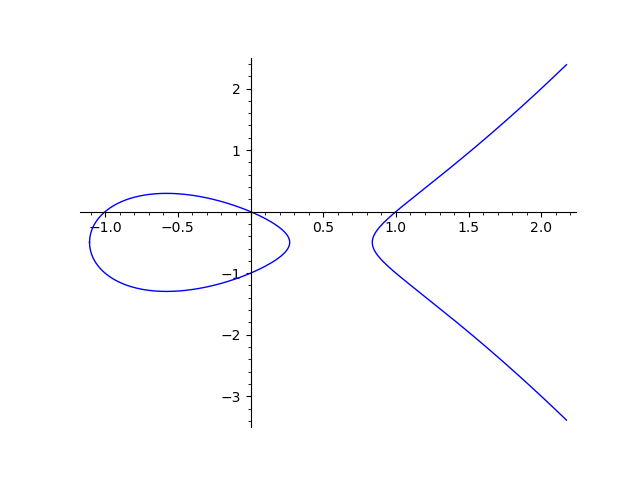
|
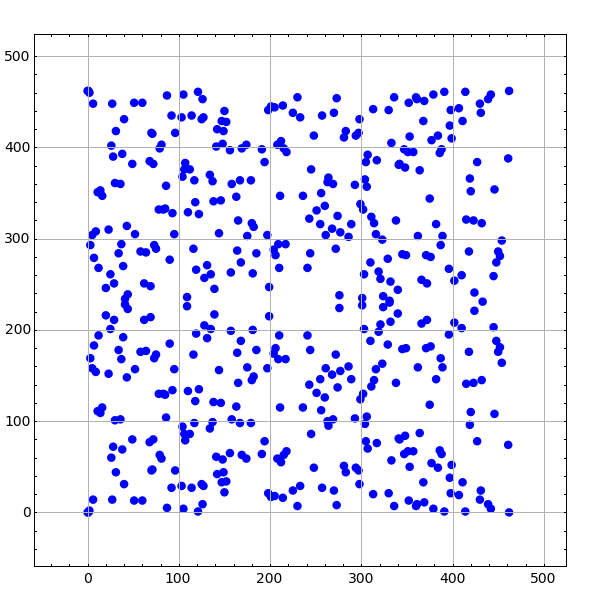
|
Analysis of List of random number generators
-
Linear Congruential Generators (LCG) - Defined by the recurrence $X_{n+1}=(aX_n+c)\mod m$. This type of generator
is very widely used, and when $c$ is coprime to $m$ and $a$ is a generator mod $m$, the period will be high
($\frac{m}{4}$ to $m$ depending on various things).
glibc, Visual C++,musl, Java, and POSIX all use this type of prng. Reversing such a generator with known $a$, $c$, and $m$ is almost trivial. We can rewrite the recurrence as $$\begin{pmatrix} X_{n+1} \\ 1 \end{pmatrix} = \begin{pmatrix} a & c \\ 0 & 1 \end{pmatrix} \begin{pmatrix} X_n \\ 1 \end{pmatrix} \mod m$$ and then as $$\begin{pmatrix} X_{n+k} \\ 1 \end{pmatrix} = \begin{pmatrix} a & c \\ 0 & 1 \end{pmatrix}^k \begin{pmatrix} X_n \\ 1 \end{pmatrix} \mod m.$$ This means once we find the internal state of the generator at any $n$, we can find its state (and in turn the number it will generate) at any future $n+k$. Depending on how a program uses such a prng, it may take many observations to find the internal state $X_n$ at some point. We would essentially build up a lot of equations involving the matrix until we could uniquely determine it. Like if the program only takes 5 bits out of this prng at a time and stores them in $b_n$, we would need to store $b_n = X_n \mod 2^5$ through $b_{n+13} = X_{n+13}$ to be able to uniquely determine all 64 bits of $X_n$. And in practice it's likely that some outputs of the prng would be thrown out, which could complicate this process. - Linear Feedback Shift Registers (LFSR), Mersenne Twister (MT), Xorshift/Xoroshiro, and SplitMix - These have more complicated recurrence relations than LCGs, and often larger internal states. For example, the common version of MT uses 2.5 KB of state and a recurrence relation that is represented in terms of many bitshifts and xor operations. However, the key point is that xor, bitshift, and the other operations used in these families of prngs are all linear operations, so the exact same matrix-based analysis we used on LCGs will work for these generators as well, though the matrices in question become pretty large in some cases like MT.
- Lagged Fibonacci Generators (LFG) - These are the final class of non-cryptographic prngs is wide use, and the most interesting from a mathematical perspective because these are the only class that has a commonly used nonlinear variant. The recurrence for and LFG is simply $S_n=S_{n-j}\star S_{n-k}\mod m$ where $\star$ is any binary operation. Typically, addition, subtraction, multiplication, or xor is used. We have to keep track of the previous $k$ values of $S_n$, meaning the internal state size is $kb$ where $b$ is the size of $S_n$ in terms of bits. In the case of addition, subtraction, and xor, this is ultimately a linear operation in terms of the internal state, because we can write $$\begin{pmatrix} S_n \\ S_{n-1} \\ \vdots \\ S_{n-k+1}\end{pmatrix} = \begin{pmatrix}\cdots S_{n-j}\star S_{n-k}\cdots \\ \hline\begin{array}{c|c} I_{k-1} & \vec{0}\end{array}\end{pmatrix} \begin{pmatrix}S_{n-1} \\ S_{n-2} \\ \vdots \\ S_{n-k}\end{pmatrix} \mod m$$ where the first row in the matrix represents the linear equation for $S_n$ in terms of $S_{n-j}$ and $S_{n-k}$, and the rest of the matrix simply brings over $S_{n-1}$ through $S_{n-k+1}$ (hence the identity). The reason this fails to work for multiplicative LFGs is simply because multiplication is not linear. We'll see what we can do about that in the next section.
But what if there was a way to make Multiplication Linear 🤔
Since we are working mod $m$ though, we are working in a finite order group so we can use the discrete logarithm! The group of integers mod $m$ under multiplication is a particularly well understood group, and most discrete logarithm algorithms are either general purpose (eg Baby-step Giant-step and Pohlig-Hellman) or specialized to $Z_m^*$ (the integers mod $m$ under multiplication).
The most fundamental facts about $Z_m^*$ are:- $Z_m^*$ has $\varphi(m)$ elements, where $\varphi(m)$ is Euler's Phi function, which counts the number of integers from $0$ to $m$ which don't have any factors in common with $m$ (other than $1$). This is a consequence of Bezout's identity, which tells us that for any $(x,y)$ there is a solution to $ax+by=\mathrm{gcd}(x,y)$. If we set $y=m$, then Bezout tells us that there is an inverse $a$ of any $x$ whose gcd with $m$ is $1$.
- $Z_{ab}^*\cong Z_a^*\times Z_b^*$ when $\mathrm{gcd}(a,b)=1$. This is a consequence of the Chinese remainder theorem, and it means that we can treat the multiplicative group mod a composite number as the Cartesian product of the multiplicative groups mod $p^k$ for all primes $p$ dividing $m$, where $k$ is the maximal power for each $p$.
- $\varphi(ab)=\varphi(a)\varphi(b)$ when $\mathrm{gcd}(a,b)=1$. This is a consequence of the previous fact, although it would normally be proved first. This reduces the problem of finding $\varphi(m)$ to the problem of factoring, and finding $\varphi(p^k)$. The second problem is easy, $\varphi(p^k) = p^k - \#\{ap|a\in\{0,\ldots,p^{k-1}\}\} = p^k - p^{k-1} = (p-1)p^k$. The first problem is hopefully hard unless you are the owner of a large quantum computer, otherwise a lot of cryptography is in trouble.
-
$a^{\lambda(m)} = 1 \mod m$ when $\mathrm{gcd}(a,m)=1$. $\lambda(m)$ is the Carmichael
function, and it is defined by $\lambda(ab)=\mathrm{lcm}(\lambda(a),\lambda(b))$ and
$\lambda(p^k)=\varphi(p^k)$ for prime powers, unless $p=2$ and $k>2$ in which case $\lambda(2^k)=\frac{1}{2}\varphi(2^k)=2^{k-2}$.
This solidifies the obvious fact that $a^n \mod m$ is periodic (it must be periodic because it only has finitely many values and $a$ has an inverse) by telling us its period must divide $\lambda(m)$. The minimal positive power of $a$ such that $a^n = 1 \mod m$ is called the "order" of $a$ ($\mathrm{ord}(a)$).
Any $a$ with order $\lambda(m)$ is called a "generator" because before its sequence of powers repeats, it generates all elements of $Z_m^*$. For example, consider $3 \mod 7$: $3^0=1$, $3^1=3$, $3^2=9=2$, $3^3=27=6$, $3^4=81=4$, and $3^5=243=5$. $3^6=729=1$ as expected.
- $m$ has $\varphi(\varphi(m))$ generators if $m=2$, $4$, $p^k$, or $2p^k$ where $p$ is an odd prime. Otherwise, $m$ does not have any generators.
We are trying to investigate the equation $S_n=S_{n-j}\cdot S_{n-k}\mod m$. When generators exist mod $m$, if $g$ is a generator then we can rewrite this equation as $g^{\ell_n}=g^{\ell_{n-j}}g^{\ell_{n-k}}\mod m$, or equivalently $\ell_n=\ell_{n-j}+\ell_{n-k}\mod \lambda(m)$. So we successfully make LFMs linear! With several caveats, sadly.
With Several Caveats: Baby Steps
Enter the Baby-step Giant-step algorithm. This is a general purpose method for solving the discrete log problem in any group, and it's one that's fairly rediscoverable. Notice that we can rewrite $h=g^x\mod p$ as $hg^{-x}=1\mod p$ because $g$ is invertable. We could also write $x=a+b$ and have $hg^{-a}=g^b\mod p$. But we know $x$ is at most $\lambda(p)-1=p-2$. So we can force $a$ to be a multiple of $d=\lceil\sqrt{p-2}\rceil$, and create a list of values of $hg^{-a}\mod p$ and compute values of $g^b\mod p$ until we find an overlap. Since any value of $x$ can be broken into $kd+b$ where $k$ and $b$ are both at most $d$, this lets us find $x$ in $O(\sqrt{p})$ instead of $O(p)$. Moreover, whenever $h$ is actually a power of $g$ mod $m$, this works for composite $m$ as well.
For example, consider trying to solve $2=3^x\mod 17$. We know $\lambda(17)=16$, so $d=\sqrt{16}=4$. $6\cdot 3=18=1\mod 17$ so $3^{-1}=6$, so $3^{-d}=6^4=4$. We make lists of $2(6^d)^k\mod 17$ and $3^b\mod 17$:
| $k$ | $0$ | $1$ | $2$ | $3$ |
| $2\cdot 4^k$ | $2$ | $8$ | $15$ | $9$ |
| $b$ | $0$ | $1$ | $2$ | $3$ |
| $3^b$ | $1$ | $3$ | $9$ | $10$ |
Stepping up the Ladder: Pohlig-Hellman for $\lambda(m)=p^k$
Enter the Pohlig-Hellman algorithm. This one is less simple, less general, and less easy to understand. It's not impossible to rediscover, but it would require strong knowledge of group theory to do so. PH depends on the factorization of the order of the group. First, consider numbers $m$ for which generators exist and $\lambda(m)=p^k$ for some prime power $p^k$.
We want to find $x\mod p^k$ such that $h=g^x\mod m$. Obviously if we know $x$ mod $p^k$ then we know it mod $p^{k-1}$, but is it possible to work the other way? In fact it is, and that idea is the crux of PH (and many other number theoretic algorithms). If $x=r\mod p^{k-1}$, then $x=ap^{k-1}+r\mod p^k$ for some $a\in\{0,\ldots,p-1\}$. $g$ has order $p^k$, so $g^{p^{k-1}}$ has order $p$. We then apply this method of decreasing the order of an element to $h(g^{-1})^x=1\mod m$.
At first, we don't know anything about $x$, but we know $h(g^{-1})^{p^{k}}=1\mod m$. This means $\mathrm{ord}(h(g^{-1}))$ divides $p^k$, but that's true for every element of $Z_m^*$. What's much more interesting is that $\mathrm{ord}\left(h(g^{-1})^{p^{k-1}}\right)$ divides $p$. Because $g$ is a generator, there are $p-1$ choices of $x_1$ such that $\mathrm{ord}\left(h(g^{-x_1})^{p^{k-1}}\right)=p$, but only one $x_1$ for which $\mathrm{ord}\left(h(g^{-x_1})^{p^{k-1}}\right)=1$. By definition, $1$ is the only element with order $1$.
This is already enough to solve $h=g^x\mod m$ for $x$ where $\lambda(m)=p^k$ in $O(kp)$ time. We define a sequence $x_0$, $x_1$, $\ldots$, $x_k$ where each $x_i = ap^{i-1}+x_{i-1}\mod p^i$ for some $a\in\{0,\ldots,p-1\}$. Each $x_i$ also satisfes $(h(g^{-x_i}))^{p^{k-i}}=1\mod m$, which allows us to identify the correct $a$ at each step. However, we can slap baby-step onto this to make it $O(k\sqrt{p})$.
Instead of $x_i = ap^{i-1}+x_{i-1}\mod p^i$, write $x_i = (ad+b)p^{i-1}+x_{i-1}\mod p^i$ where $d=\lceil\sqrt{p}\rceil$. Then we have $$\left(h\left(g^{-adp^{i-1}-bp^{i-1}-x_{i-1}}\right)\right)^{p^{k-i}}=1\mod m$$ $$\left(h\left(g^{-adp^{i-1}-x_{i-1}}\right)\right)^{p^{k-i}}\left(g^{-bp^{i-1}}\right)^{p^{k-i}}=1\mod m$$ $$\left(h\left(g^{-adp^{i-1}-x_{i-1}}\right)\right)^{p^{k-i}}=\left(g^{bp^{i-1}}\right)^{p^{k-i}}\mod m$$ $$\left(h\left(g^{-adp^{i-1}-x_{i-1}}\right)\right)^{p^{k-i}}=\left(g^{p^{k-1}}\right)^b\mod m$$ Just like with the baby-step giant-step algorithm, now we can create lists of values for both sides for $a$ and $b$ in $\{0,\ldots,d-1\}$ and check for an overlap. This takes $O(\sqrt{p})$ time, leading to the $O(k\sqrt{p})$ time overall algorithm we were looking for.
One Foot on each Ladder: PH for $\lambda(m)$ with multiple prime divisors
It turns out this is possible: $g_a=g^\frac{\lambda(m)}{a}$ has order $a$. In our simplified setting, this is just $g^b$, but if $\lambda(m)$ had more prime power factors than just $a$ and $b$, raising $g$ to the product of all prime power factors besides $a$ would get us our element with order $a$. Then for each prime power divisor $a=p^k$, we also define $h_a=h^\frac{\lambda(m)}{a}$ and then simply solve $h_a=g_a^{x_a}\mod m$ using the above algorithm (PH for $\lambda(m)=p^k$). $x_a$ lives mod $a$, since raising $h$ and $g$ to $\frac{\lambda(m)}{a}$ decreases their maximal order from $\lambda(m)$ to $a$, which is why that algorithm can be applied.
Then, once we have $x_a\mod a$ for each prime power divisor of $\lambda(m)$, we simply use the Chinese remainder theorem to combine them into one $x\mod \lambda(m)$ which solves $h=g^x\mod m$ as desired.
The Remaining Caveats: Factorization and some Groups without Generators
Factoring is very strongly believed to be a hard problem for anyone who doesn't have a (by current measures) comically large quantum computer. We can find factors quickly for numbers which have sufficiently small factors, numbers which are very close to a perfect square, some other special cases, and any number which is below about 100 digits.
When $Z_m^*$ has generators, it has $\varphi(\varphi(m))$ of them, so picking numbers mod $m$ will get us a generator in constant expected time.
Finally, $Z_m^*$ only has generators if $m$ is $2$, and odd prime power, or twice one of those, and more complicated groups also are not at all guaranteed to have generators. To cap things off, we'll look at how we can get around this for one of the most common groups in cryptography: $Z_{2^k}^*$.
Discrete Logarithm mod Powers of 2
However, $Z_8^*$ is a curious case. It consists of the numbers $\{1,3,5,7\}$ mod $8$, and something very disturbing happens: $3^2=5^2=7^2=1$. That is to say, all elements of $Z_8^*$ have order $1$ or $2$, so there are no generators (which would have order $4$ in this case). Alas! My beautiful Pohlig-Hellman algorithm is ruined for any power of $2$ larger than $8$, because a generator in any of these groups would imply a generator mod $8$ and we just saw there isn't one!
$Z_8^*$, instead of being equivalent to $Z_{\lambda(8)}$, is equivalent to a group called the Klein 4 group, which is in turn equivalent to $Z_2\times Z_2$. And for powers of $2$ larger than $8$, we notice that we have a different way of expressing this group: $\{1,2^{k-1}-1,2^{k-1}+1,-1\}$ under multiplication mod $2^k$. We can easily check that each of the last three elements squares to $1$ and the multiplication table for this group matches the multiplication table for $Z_8^*$.
Next, we note that $3$ has order $2^{k-2}$ in $Z_{2^k}^*$ (we can prove this from the definition of the Carmichael function for $2^k$ and Euler's criterion, but quadratic residues are beyond the scope of this discussion). We know $Z_{2^k}^*$ has $\varphi(2^k)$ elements, and in fact any $r\mod 2^k$ can be written as $r=p^a q^b 3^x\mod 2^k$, where $p=2^{k-1}-1$, $q=2^{k-1}+1$, $a$ and $b$ can both be $0$ or $1$, and $x$ lives mod $2^{k-2}$. We know this works because $p$ and $q$ have order $2$, $3$ has order $2^{k-2}$, and $p$ and $q$ generate the embedding of $Z_8^*$. So we know the group generated by $p$, $q$, and $3$ has an order which is a multiple of $2^{k-2}$ and divides $2^{k-1}$ while being strictly larger than $2^{k-2}$, so it must be $2^{k-1}$.
This means that to "solve" the discrete logarithm problem mod $2^k$, instead of being able to just solve $h=g^x\mod 2^k$, we have to try solving $h=p^a q^b 3^x\mod 2^k$ for all four possible choices of $p^a q^b$ until one of them works. A simple modification once we know what to do, and possibly one that could be improved via a similar strategy to PH, but it took a lot of preparation to understand the problem well enough to reach this point.
Reverse-Engineering a LFM's Seed
And the final piece is being able to find all $a$, $b$, and $x$ needed to reconstruct the last $k$ values of $S$ (the internal state of the LFM prng). Fortunately, this is exactly what the previous section "Discrete Logarithm mod Powers of 2" allows us to do!
Here is a small function that computes $a$, $b$, and $x$ given $h=S$.
const uint64_t cr8r_prng_2tg_t64[4] = {1, (1ull << 63) + 3, (1ull << 63) - 1, -1};
// raise b to the power of 2**i mod 2**j
inline static uint64_t pow_ti(uint64_t b, uint64_t i){
while(i--){
b *= b;
}
return b;
}
uint64_t cr8r_prng_log_mod_t64(uint64_t h){
uint64_t y = pow_ti(3, 61);
// the inverse of 3 mod 2**64
uint64_t g1 = 12297829382473034411ull;
for(uint64_t gi = 0; gi < 4; ++gi){
uint64_t x = 0;
uint64_t b = h*cr8r_prng_2tg_t64[gi];
// maintain g1_ti = g1**(2**i)
uint64_t g1_tk = g1;
uint64_t k = 0;
for(; k < 62; ++k){
uint64_t hk = pow_ti(b, 61 - k);
if(hk == 1){
// x is not modified
}else if(hk == y){
x |= 1ull << k;
b *= g1_tk;
}else{
break;
}
g1_tk = g1_tk*g1_tk;
}
if(k == 62){
// x was successfully extended to 62 bits, set the high 2 bits
// to the powers (0 or 1) of the order-2 generators 2**63+1 for
// the highest bit, and 2**63-1 for the second highest bit.
return (gi << 62) | (x&((1ull << 62) - 1));
}
}
// reachable iff h is even
return 0;
}
Finishing Thoughts
Because of this, we could make a LFM that could not be reverse engineered, at least not via these methods, by choosing $m$ more carefully so that $m$ is still a prime power or twice a prime power but $\lambda(m)$ is a large prime or the product of two large primes not too close to each other.
These classes of prngs are intended for speed and not security though, so when they are used properly, being able to invert them like this is not harmful. If security is important, a cryptographic prng should be used instead.